Whether you are new to the industry or are well seasoned and want to review some of the basic information that you learned in the past, these courses and lessons will clearly outline what you are looking for. “Power Systems Electric” is On-Line training that bridges the gaps between textbook theories and practical power systems experience. As a retired electrical engineer who has gone through the experience of developing a career in electrical power systems, I know how frustrating it can be to try and find the answers, so I put together these courses that I feel would have been a major help to me in my development. I have also taken suggestions from students of what they would like to see in addition to these courses which I have given live in person.

Basic Electrical Learning

For those new to the industry, there is a beginner’s group of courses that cover the “Fundamentals of Electricity ” including DC and AC Circuit Analysis. These lessons examine such basics as Ohm’s Law, Series, and Parallel Circuits. The first, and perhaps most important, relationship between current, voltage, and impedance, “Ohm’s Law”, and its relevance to Series and Parallel Circuits. Subsequently, this will lead to the development of Kirchhoff’s Laws as they help to further analyze Network Analysis & Metering Circuits.

Conductors and Insulators are investigated along with their connected components, Capacitors, Inductors, and how they are influenced by Electromagnetism.

Alternating Current (AC – an electric current that periodically reverses direction) is the form in which electric power is delivered to businesses and residences, and it is the form of electrical energy that consumers typically use when they plug kitchen appliances, televisions, fans, and electric lamps into a wall socket.

The abbreviations AC and DC are often used to mean simply alternating and direct, as they are applied to current or voltage.

These AC courses deal specifically with sinusoidal waveforms and will provide the student with the basic understanding of working with circuits involving Alternating Current, which includes sinusoidal waveforms, vectors & phasors, reactance & impedance of R,L,C circuits, as they relate to the basic laws and theorems of electricity. This includes working with AC Power, Power Factor, Resonance, Complex Numbers, Reactance, and Impedance

Advanced Electrical Learning

These Courses involve subjects such as “Short Circuit Analysis for HV Three-Phase Systems ” which introduces the student to the basic concepts of fault studies on a high voltage three-phase system. System modeling is then used in order to aid in this process, with the ability to move between asymmetrical and symmetrical systems. With hey Searle and extensive study of “Per Phase” & “Per Unit” methodologies system faults are analyzed with the use of symmetrical components.

“A Per-Unit System ” is the expression of system quantities as fractions of a defined base unit quantity. Calculations are simplified because quantities expressed as per unit do not change when they are referred from one side of a transformer to the other.

In these courses, you will learn exactly what Per Unit Analysis is, the main advantages of using it, how manufacturers of equipment use and rate their products, and the technique of converting to and from the Per Unit system.

Several examples of working with Per Unit are demonstrated in this crisp clear presentation. When you finish you will have a though understanding of this subject.

It is important for all power engineers and technicians to be familiar with the concept of Per Unit as it is being used and referred to every day in power flow, short circuit evaluation, and motor starting studies.

The method of “Symmetrical Components ” is used to simplify asymmetrical three-phase voltages and current analysis by converting the unbalanced system into two sets of balanced phasors and a set of single-phase phasors, or symmetrical components. These sets of phasors are called the positive, negative, and zero sequence components.

An understanding of this method is essential for the understanding of fault analysis and modern-day protection schemes. These courses will provide you with the knowledge to comprehend the concept and how it is applied.

Supplemental Electrical Lessons

In all power electrical analyses, the student will encounter special Trigonometric and Mathematical identities and equations. This site contains special supplemental lessons that zero in on those identities and equations. For example, there are lessons that take you from the “Fundamentals of Trigonometry ” to the more sophisticated requirements in electrical engineering. As you work and study in electrical engineering you are going to run into proofs and equations that are based on trigonometry. A good example of this is when studying AC current, voltage, and impedance calculations, phasors or vectors are used and combined mathematically. Further adventures into complex power will also require a knowledge of trig functions and identities. As a student of this course, you will be introduced to these or at least re-introduced to these that may have been long since forgotten.
In mathematics, “The Derivative of a Function ” of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object’s velocity: this measures how quickly the position of the object changes when time advances.

Specialized Electrical Lessons

Specialized lessons include the “Protection & Control(P & C)” principles of high voltage stations. HV Bus Differential Protection is studied along with restrictions due to CT saturation & mismatch and its solution, “Restraint Differential Protection”.

High Voltage Circuit Breakers are examined as to the various Types (Oil, Vacuum, Air Blast, SF6), their Controls as well as the introduction of potential transformers & current transformers, and their use in conjunction with the relevant instruments such as ammeters, voltmeters, watt meters, and energy meters.

Other lessons include the study of “Transformers ” including core construction along with losses, cooling, and mitigation techniques. Three-phase transformer configurations are studied along with harmonic distortion, CT saturation, and on-load tap-changer problems and how these problems are dealt with. Over-current and restraint differential transformer protection is developed along with a look at some examples of ” Old School relays” as well as modern IDE (intelligent Electrical Devices) relays.

Transformer Connections: (Y – Y; Delta – Delta; Y – Delta; Delta – Y & Y – Zag Zig) are examined along with Transformer Clock System Vector Nomenclature.

Lastly, there is a special section dedicated to “Single and Three-Phase Metering “, including old analog and new digital kilowatt-hour meters.

Conclusion

Regardless of whether or not you are new to the industrial power system, you’ll find what you’re looking for on this site in the way of training. In order to review or select any of these courses, left-click on any of the blue highlighted hyperlinked words of this posting or on “14 Courses Available” from the top menu of the landing page. All of the courses have a free introduction

As a bonus and in the way of a thank you, for your interest in PSPT’s WEB (and Blog) page, I’m making available my 50-page “Electrical Power” crib sheets. These were prepared for use with my courses that are available on this site. There is one section associated with each course and is extremely valuable while viewing the course, as well as a recall of the pertinent formulas and information after the fact. The contained information is also useful during any technical career as a quick reference from time to time. Simply click here or on the picture to the right to be taken to where you can download this item.

September 26, 2022

Blog #9 - Residential Electrical Power Chapter Four

September 26, 2022/ Graham VanBrunt

Residential Electrical Power Chapter Four

Low Voltage Circuit Wire & Cable

In the world of building wire, there are several common choices available that at first appear quite similar. Some of the most common of them; THHN, THWN, and Romex.

THHN WIRE is Thermoplastic High Heat-resistant Nylon-coated wire that is a single conductor wire with PVC insulation and a nylon jacket. It’s commonly used in conduit as electrical wire for buildings. Its heat and oil resistance makes it suitable for appliances and machine tools.

THWN is essentially the same as THHN and the two are often used interchangeably. THWN is also a single conductor wire with PVC insulation and a nylon jacket. The key difference is the “W” in the name which indicates water resistance. THWN is rated for temperatures up to 90°C in wet conditions vs 75°C for THHN.

Romex wire refers to the trade name for Thermoplastic-Sheathed Cable (TPS). Romex is often used as residential wiring for electrical circuits and lighting. We generally think of a specific type of Romex, which is known for its nonmetallic sheathing and primary use as branch wiring. This is referred to as Romex NM-D or B.

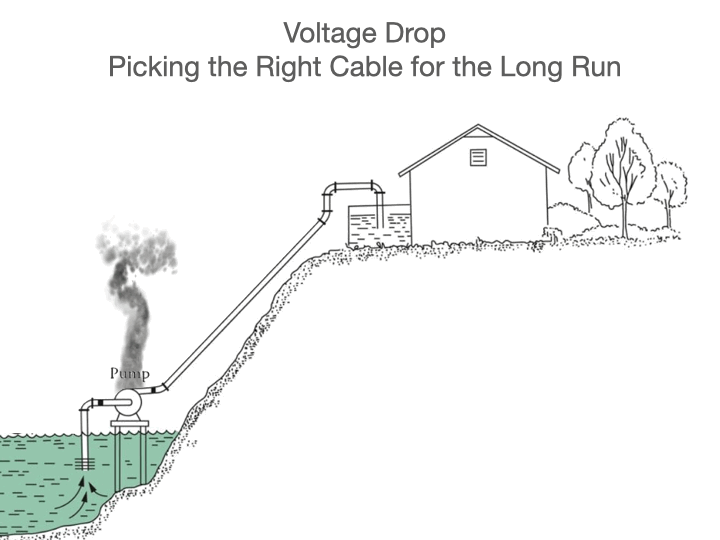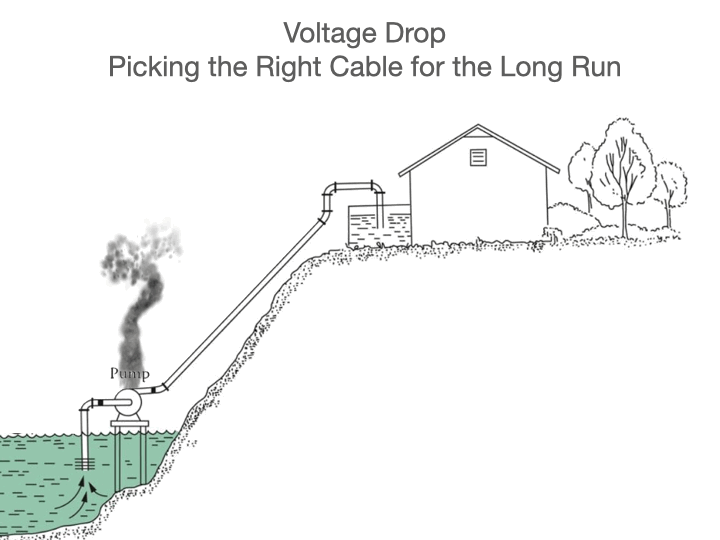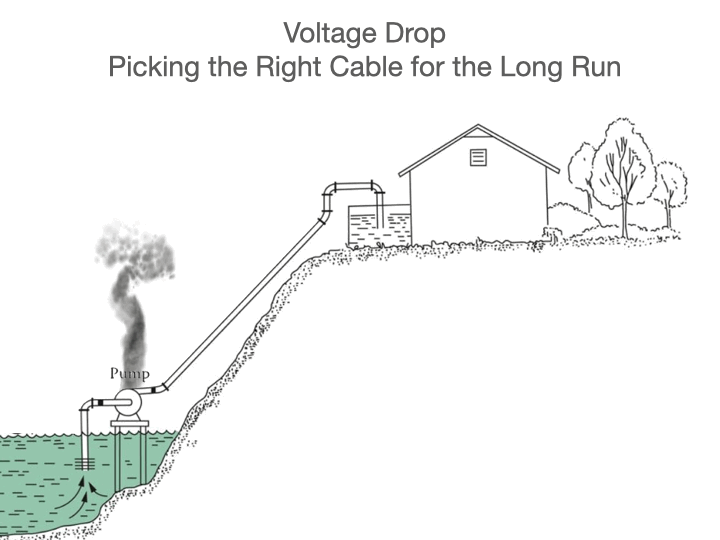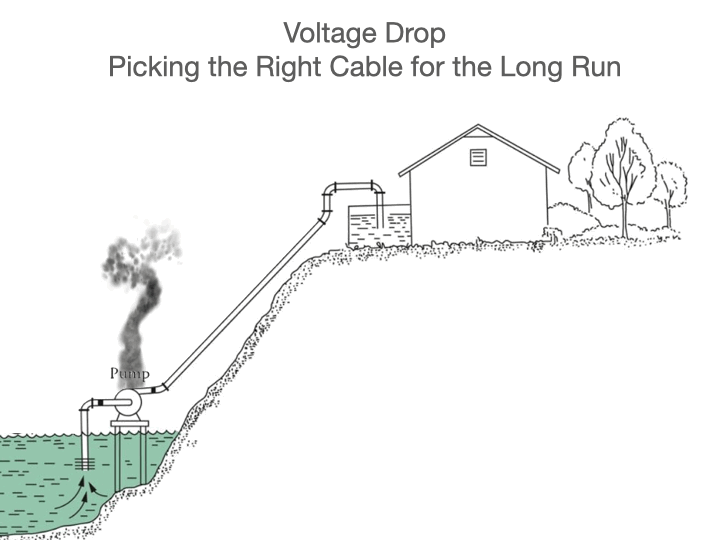
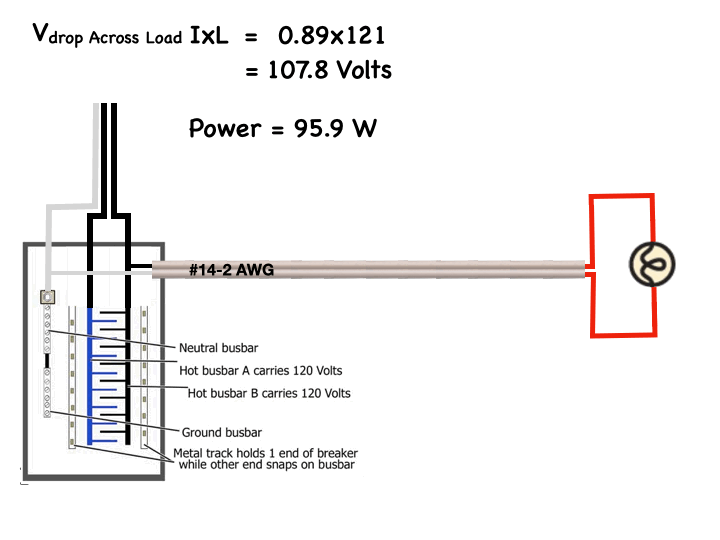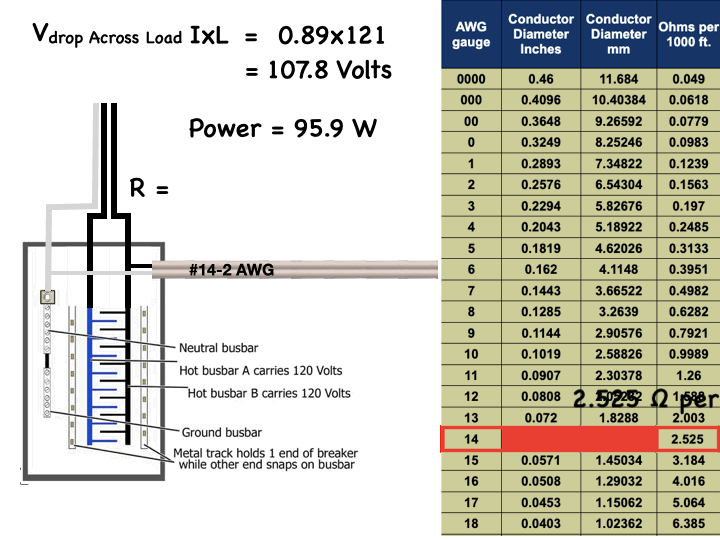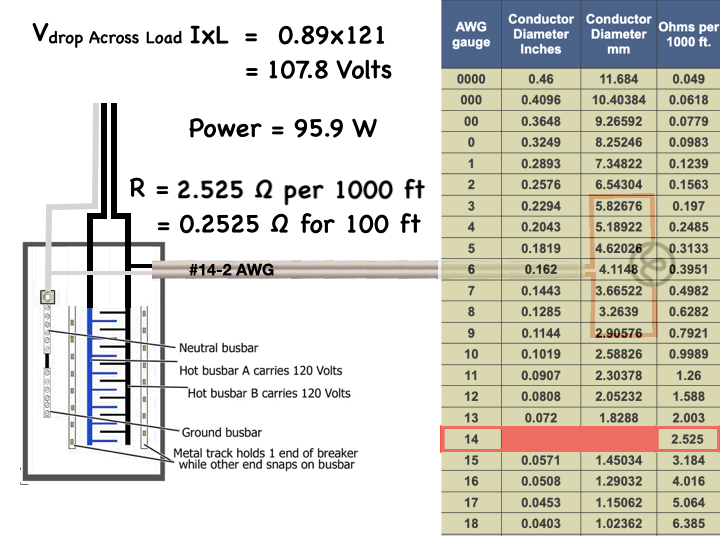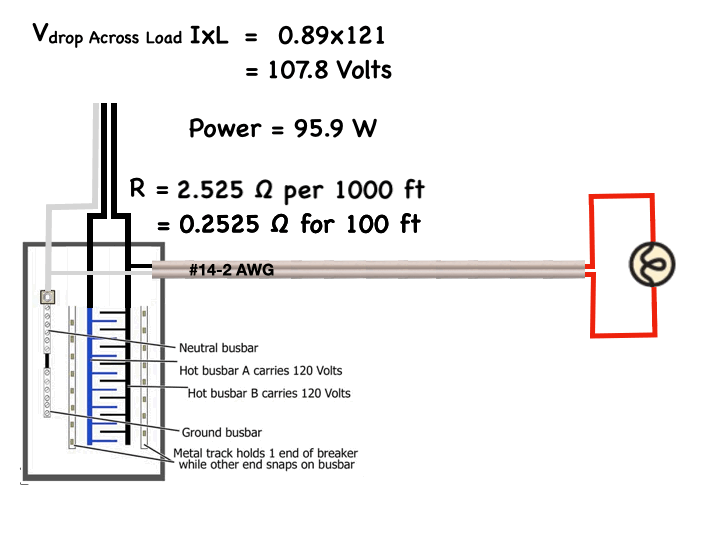
Recently, Nexans Canada introduced colour coding to its line of non-metallic sheathed cables to enable easy identification of the various sizes commonly used in residential construction. These copper conductor cables are used mainly to distribute power to outlets, lights, electric ranges, dryers, and other equipment. This type of cable is commonly known by trade names such as Romex or Canadex, but the Canadian Standards Association type is NMD90, meaning non-metallic, dry location, 90 degree Celsius rated.

Nexans now supplies NMD cable with coloured jackets. Cable for use with 15 ampere AFCI is supplied with a blue jacket, and the cable for use with a 20-ampere kitchen GFCI has a yellow jacket. As well, two conductor No. 14 AWG copper NMD used for other 15-ampere circuits is supplied with a white jacket, all No. 12 AWG copper for 20-ampere circuits has a yellow jacket, all No. 10 AWG copper for 30-ampere circuits has an orange jacket, and cables for over 30 amperes have a white jacket.

The jacket colour coding is not required by any electrical code or by CSA product requirements. However, Nexans supplies the colour-coded products as an aid for installers and inspectors in identifying cables used to supply the two special types of circuits mentioned above and to indicate copper conductor size. In doing so Nexans makes the job of cable identification quick and accurate for the contractor and inspector.

NFPA 70 National Electrical Code

(NEC)

2020 Edition 1st Edition

by (NFPA) National Fire Protection Association

Based on the 2020 National Electrical Code (NEC), the National Electrical Code Handbook clarifies concepts for a better understanding of the Code. It's a powerful communication tool that helps you explain the NEC to clients and others who might not have professional electrical training.

Voltage drop is the reduction in voltage in an electrical circuit between the source and the load. Wires carrying electricity have inherent resistance, or impedance, to current flow. Voltage drop is the amount of voltage loss that occurs through a circuit due to this impedance.

For equipment to operate properly, it must be supplied with the right amount of power, which is measured in watts which is calculated by multiplying current (amps) x voltage (volts). Motors, generators, lights — anything that runs on electricity — is rated for power. The correct amount of power enables equipment to meet its designed power rating and operate efficiently. Too much or insufficient amounts of power can result in inefficient operation, wasteful power usage, and even equipment damage. That is why understanding voltage drop calculations and selecting the correct cable for each application is so important.

The National Electrical Code (NEC) catalogs the requirements for safe electrical installations and represents the primary document for guidance. Providing direction for both trained professionals and end users, these codes set the foundation for the design and inspection of electrical installations. For branch circuits, look to NEC advises that conductors for feeders to dwelling units should be sized to prevent voltage drop exceeding 3% and maximum total voltage drop on both feeders and branch circuits should not exceed 5% for “reasonable efficiency of operation.”

In addition, when dealing with sensitive electronic equipment. It states that voltage drop on any branch circuit shall not exceed 1.5% and the combined voltage drop on branch circuit and feeder conductors shall not exceed 2.5%. It is important to note that much of the equipment manufactured today contain electronics that are particularly sensitive to excessive voltage drop.

Ampacity, a cable’s electric current-carrying capacity, is also connected to voltage drop. Electrical Codes stress the importance of accounting for voltage drop when considering a cable’s ampacity rating and the need to satisfy both requirements.

In order to understand voltage drop let’s consider the simple circuit in the diagram to the right. A voltage source of 110 Volts AC is connected to a load resistor of 11 Ω. According to Ohm's Law the current that will be drawn by the load will be equal to the voltage divided by the resistance, which in this case will be 10 Amps.

Looking at the same components, but this time with two 11 Ω resistors in series with each other. We still have a voltage supply of 110 Volts and Ohms Law tells us that current will be 5 Amps and the voltage drop across each resistor will be 5×11 for 55 Volts.

Let's add eight more resistors, and reconfigure the circuit to look like this. The current in a circuit will now be a function of the supply voltage divided by the total resistance which is made up of ten 11 Ω resistors. Using Ohms Law to obtain a current in a circuit we use the supply voltage, divided by the total resistance; substituting actual values we get 110 volts divided by 110 Ω or 1 amp.

We can easily calculate the voltage drop across each resistor now by multiplying the current times the individual resistance of 11 Ω which works out to 11 Volts.

Now let's add a load of 10 Ω to the circuit. The total load now becomes the 10 resistors plus the 10 ohms of the load. The current of the circuit is now given by 110 Volts divided by 110 ohms plus the load of 10 Ω which equals 0.92 Amps.

This time we are interested in the voltage drop across the 10 Ω load which is given by the current times the 10 Ω load which equals 9.2 Volts.

Let's add some realism to the situation and suppose that the load is a 100 W incandescent light bulb.

The equivalent load existence of the 101 light which is essentially just a resistor that emits light and heat, is given by the equation. Plugging in the actual values of the lightbulb if it is connected to 110 volt power supply, the equivalent resistance would be 121 Ω.

I am making one other change to our circuit and that is I'm going to change each of the individual resistors “R” to 0.25 Ω. That means the calculated circuit current will be 110 volts divided by the total resistance of 2.5+121 which equals 0.89 Amps. With that amount of current flowing in the circuit, the voltage drop across our lightbulb will be 0.89×121 which equals 107.8 volts. This is interesting now, because the lightbulb was rated at 100 W which was calculated for a supply voltage of 110 volts.

The physical make up of the lightbulb has not changed, which means our calculated resistance also has not changed, it is still 121 Ω. In our circuit, the voltage drop across the lightbulb has been calculated at 107.8 volts and the current in a circuit has been calculated at 0.89 amps, therefore the lightbulb will be the dissipating 95.9 W. This means that the output light will be reduced in brilliance by about 4 percent.

The total resistance in the circuit of 121 Ω is the same as connecting a power source to the lightbulb with a length of #14-2 AWG copper wire. This points out the fact that even copper wire has some resistance, which does become significant over some distance. Although a 4% drop in light bulb brilliance is not that significant, given more lightbulbs or more length of wire, the percentage drop across each lightbulb will decrease to a point where it starts to be significant. This becomes even more significant if the load were a motor, such as a water pump because the voltage drop across the pump is made up of both resistance and “Back EMF”. The back EMF of a motor is related to its speed of rotation, which is related to the applied voltage, so the drop in voltage is not just 4%, as in the case of a pure resistive load.

Instead of the load being purely resistive, let’s replace it with a motor whose back EMF and internal resistance provide the same voltage drop as the 10 Ω load did

This means that the voltage drop will be greater than 4%, which ultimately means more current is going to flow for the same amount of work that is being done. Over time, and depending on the time, this means the windings of the motor will begin to heat and ultimately overheat, causing damage to the motor.

Taking into consideration the characteristics of a motor, the reduction in voltage may mean that the speed of the motor does not have enough energy to get past the inrush current, exacerbating the whole situation.